Regression tests if there is a relationship between two variables where one variable (the dependent variable; commonly “Y”) logically depends on the other (the independent variable; commonly “X”).
For example, if you were to experimentally vary the width of the sidewalk and then count the number of pedestrians, one can assume a logical dependency. It is possible that varying the size of the sidewalk has an effect on the number of pedestrians, but it would not make sense to assume that the converse might be true as well: Varying the number of pedestrians certainly won’t affect the size of the sidewalk. Whenever you have an independent and a dependent variable, you need to perform a linear regression analysis.
However, if you measure two variables with no logical dependency, you need to perform a correlation analysis. For example, you could count the number of cars in the street and the number of pedestrians on the sidewalk and see if they are correlated. Both numbers (variables) do not logically depend on one another.
Usage
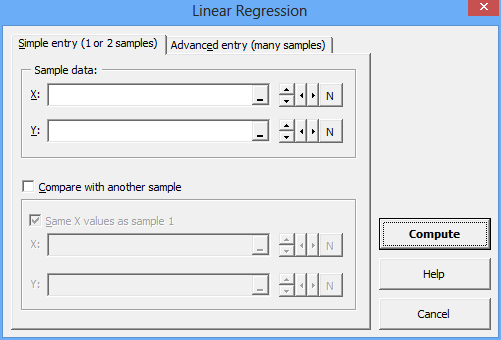
Using the Regression feature of the XL Toolbox is very straight-forward. There are two alternative methods of data entry, which are considered self-explanatory. The screenshot shows the “Simple Entry” for one or two samples.
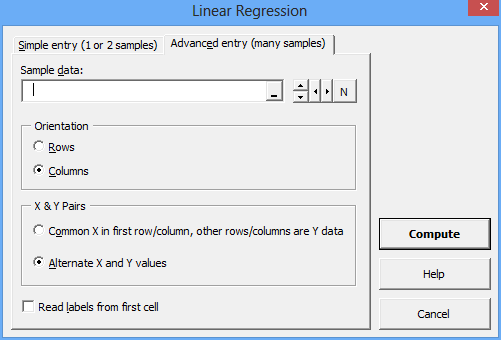
Alternatively, you can choose the “Advanced entry” method where you select an entire range of cells containing sample data. You dan indicate whether the data is organized in rows or columns, and whether there is one set of X values for several sets of Y values, or if there are several pairs of X and Y values. Check “Read labels from first cell” if the first cell in each row or column contains an informative label for the data.
Mathematical/statistical background information
The Toolbox uses the regression equations found in the excellent book by Jerrold Zar, “Biostatistical Analysis”, 4th edition, chapters 17 and 18. The Toolbox does not use simplified computational formulas.
The “Zar” is an excellent book for background reading about linear regression, correlation, and other statistical concepts. Of course, there are also many alternatives out there.